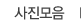아래의 일차함수 공식을 이용하여 마우스 드래그를 이용하여 배경이 움직이는 플래시를 제작해봅시다.
① 일차함수 기본 공식
※ 배경에 ‘img_mc’라는 무비클립으로 스테이지(250*200)보다 커다란(340*385) 이미지를 만들고 1프레임에 아래 스크립트를 삽입해봅시다.
<일차함수 공식>
<일차함수 공식>
x가 a부터 b까지 변할 때
y는 c부터 d까지 변한다.
=> y = (d - c) / ( b - a) * ( x - a ) + c
y는 c부터 d까지 변한다.
=> y = (d - c) / ( b - a) * ( x - a ) + c
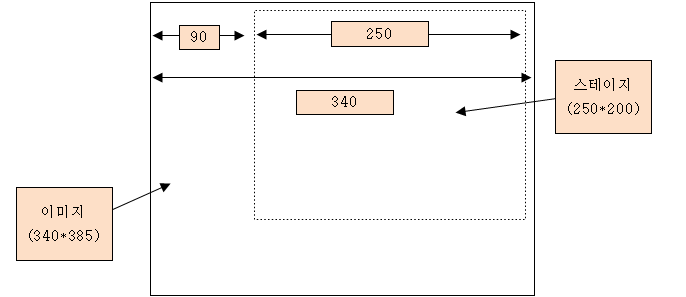
<스크립트>
_root.img_mc.onEnterFrame = function(){
// _root._xmouse가 0부터 250까지 변할 때
// img_mc._x는 0부터 -90까지 변한다!!
tx = (-90 - 0) / (250 - 0) * (_root._xmouse - 0) + 0;
this._x = this._x + 0.2 * (tx - this._x);
// _root._ymouse는 0부터 200까지 변할 때
// img_mc._y는 0부터 -185까지 변한다!!
ty = (-185 - 0) / (200 - 0) * (_root._ymouse - 0) +0;
this._y = this._y + 0.2 * (ty - this._y);
}
// _root._xmouse가 0부터 250까지 변할 때
// img_mc._x는 0부터 -90까지 변한다!!
tx = (-90 - 0) / (250 - 0) * (_root._xmouse - 0) + 0;
this._x = this._x + 0.2 * (tx - this._x);
// _root._ymouse는 0부터 200까지 변할 때
// img_mc._y는 0부터 -185까지 변한다!!
ty = (-185 - 0) / (200 - 0) * (_root._ymouse - 0) +0;
this._y = this._y + 0.2 * (ty - this._y);
}
위 소스에서 핵심은 _root._xmouse가 0부터 250까지 변할 때, img_mc._x는 0부터 -90까지 변한다는 뜻입니다. 여기에서 -90이란 숫자가 나온 이유를 알아야만 아래 문제를 해결할 수 있습니다.
※ 마우스의 움직임에 따라서 이미지가 반대로 움직여지나요? 그렇다면 올바로 제작한 것입니다. 그럼 이번에는 스테이지의 크기를 400*400으로 하고 이미지를 600*600으로 수정하여 새롭게 만들어보세요. 위 소스를 이해하셨다면 쉽게 제작할 수 있습니다.
② 돋보기 효과 만들기
가) 작은이미지(170*193)와 큰이미지(340*386)을 준비합니다.
나) 작은이미지 위 레이어에 큰이미지를 놓고 큰이미지 상위 레이어에 렌즈가 될 원형의 무비클립을 만듭니다.
다) 렌즈를 마스크 처리하고 1프레임에 아래의 스크립트를 삽입한다.
나) 작은이미지 위 레이어에 큰이미지를 놓고 큰이미지 상위 레이어에 렌즈가 될 원형의 무비클립을 만듭니다.
다) 렌즈를 마스크 처리하고 1프레임에 아래의 스크립트를 삽입한다.
/*
lens[mask]
100% 이미지
50% 이미지
*/
lens_mc.startDrag(true);
_root.big_mc.onEnterFrame = function(){
// lens_mc._x : 0 ~ 170
// big_mc._x : 0 ~ -170
_root.big_mc._x = (-170 - 0) / (170 - 0) * (_root.lens_mc._x - 0) + 0;
// lens_mc._y : 0 ~ 193
// big_mc._y : 0 ~ -193
_root.big_mc._y = (-193 - 0) / (193 - 0) * (_root.lens_mc._y - 0) + 0;
}
lens[mask]
100% 이미지
50% 이미지
*/
lens_mc.startDrag(true);
_root.big_mc.onEnterFrame = function(){
// lens_mc._x : 0 ~ 170
// big_mc._x : 0 ~ -170
_root.big_mc._x = (-170 - 0) / (170 - 0) * (_root.lens_mc._x - 0) + 0;
// lens_mc._y : 0 ~ 193
// big_mc._y : 0 ~ -193
_root.big_mc._y = (-193 - 0) / (193 - 0) * (_root.lens_mc._y - 0) + 0;
}
위 소스를 분석해보면 아래와 같습니다.
작은 이미지는 항상 보임 상태로 있고 렌즈의 영역은 마스크로 처리되기 때문에 큰 이미지에서 렌즈의 영역만큼 보이게 됩니다. 그러나 렌즈가 움직일 때 큰 바닥 이미지가 같이 움직여야 하므로 앞에서 배운 일차함수 공식을 적용하였습니다.
작은 이미지는 항상 보임 상태로 있고 렌즈의 영역은 마스크로 처리되기 때문에 큰 이미지에서 렌즈의 영역만큼 보이게 됩니다. 그러나 렌즈가 움직일 때 큰 바닥 이미지가 같이 움직여야 하므로 앞에서 배운 일차함수 공식을 적용하였습니다.














































 함수의 이해
함수의 이해